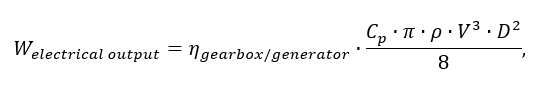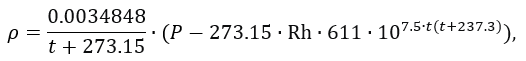Wind Energy Estimation using Statistics and Data Science

Wind energy is a vital renewable resource that plays a key role in reducing reliance on fossil fuels and mitigating climate change. As one of the fastest-growing energy sources, it provides a clean, sustainable, and cost-effective alternative for electricity generation. Advances in turbine technology, offshore wind farms, and grid integration have significantly improved efficiency and scalability.

Project Objectives and Expectations

• ▶ Classify given location based on wind power.
• ▶ Identify the optimal wind direction for installing a wind generator.
• ▶ Determine calmest and most windy months.
• ▶ Estimate amount of wind energy based on a given scenario and available technology.

Project Set-up

For this research we will use the measurements enquired by the Weather Station WS2910, which registers the following parameters:

✔ Temperature
✔ Humidity
✔ Solor
✔ Wind Speed
✔ Wind Gust
✔ Wind Direction
✔ Rain Rate
✔ Pressure

Data Overview & Visualization

The data was collected over a nine-month period starting in May 2024. The graphs below illustrate the overall trends in temperature and wind changes over time, along with their distributions.

Temperature & Pressure

Temperature Distribution

Wind Speed & Direction

Wind Direction Distribution

Key observations & insights:

• ●Based on temperature distribution one can cluster the year into two distinct seasons.
• ●Cold seasons - where temperature is normally distributed around 0℃.
• ●Warm seasons - where temperature is normally distributed 13℃.
• ●The wind direction can be divided in two main categories:
• ➯East - with values normally distributed around 125°.
• ➯West - with values normally distributed around 272°.
• ●The average wind speed at the height 0.5m above the ground over a given time frame is 1.03m/s.

Wind Power Classification

For this project we will be suing the Wind Power Classification (NREL Standard), which categorizes locations based on their average wind speed and power density at a specific height. Before that however, we need to approximate the wind speed at height 50m above the ground given the wind speed measured at 0.5m. To achieve it the following equation will used:

where v₁ is a reference speed measured at height h₁; v₂ is a wind speed at height h₂; z₀ is the roughness length, which for thid research is equal 0.1. More information can be found here.

The average approximated wind speed at the height 50m is therefore 4.8m/s, which means that given location can be classified as Class 2 - marginal.

Wind Energy Estimation

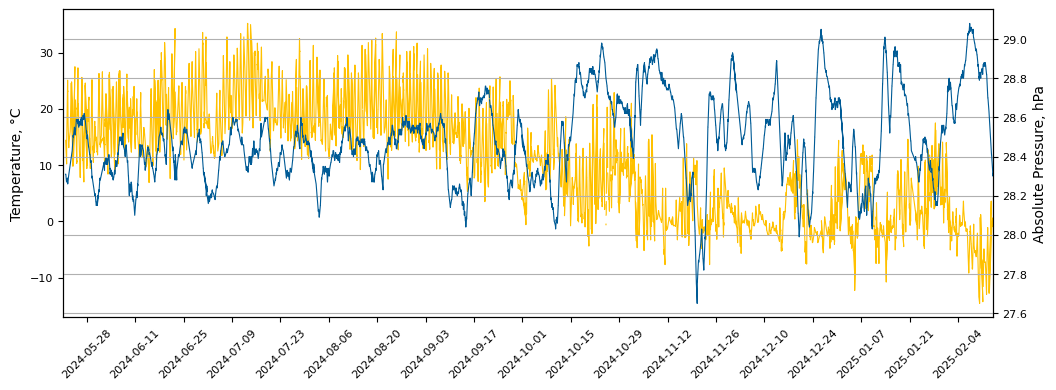
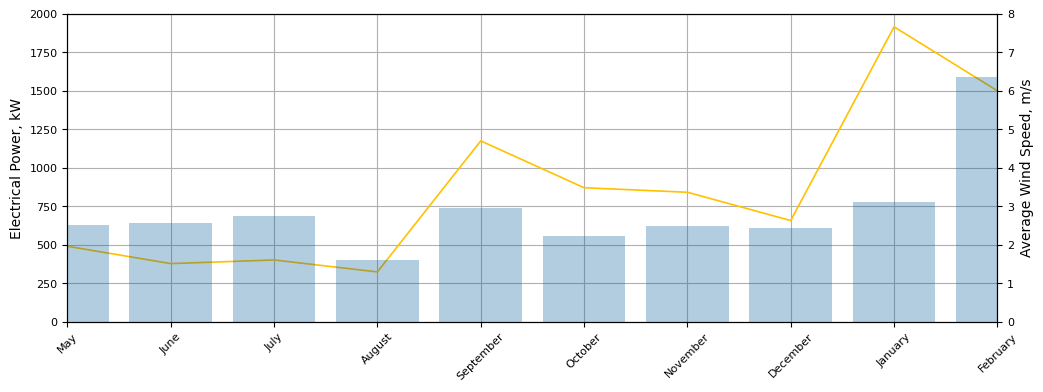
Data indicates that January is a month with the highest wind activity, while August is the lowest. This pattern is also reflected across seasons, with winter being the windiest time of the year. This aligns perfectly with electricity consumption trends, as energy usage significantly increases during colder months.

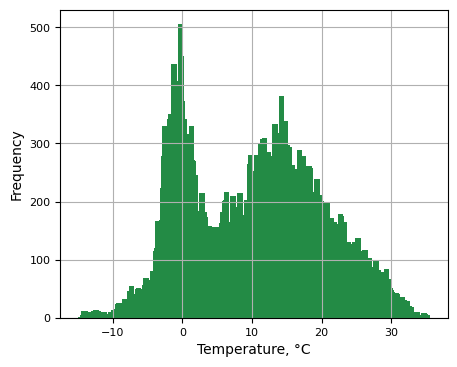
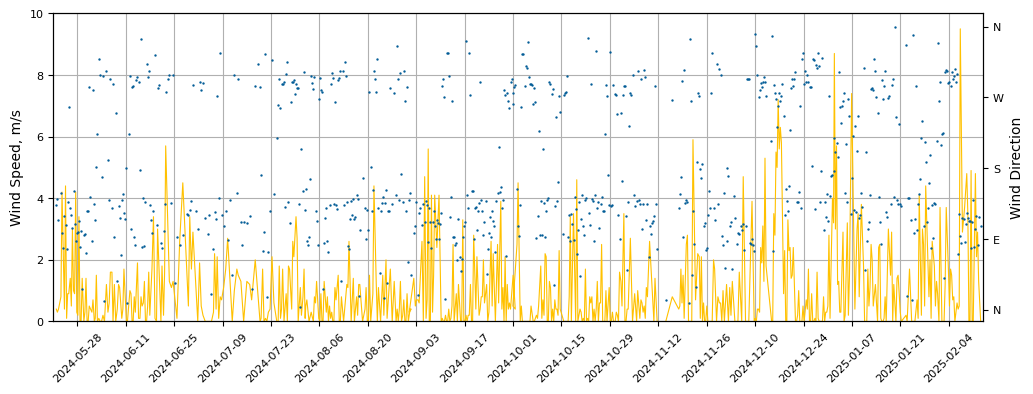
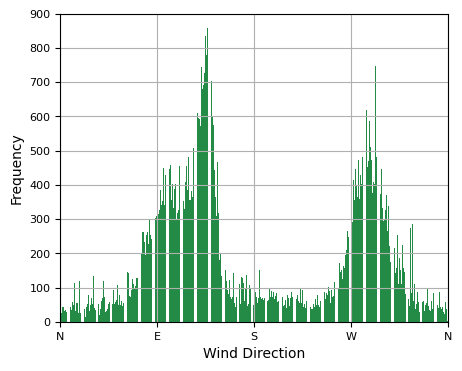
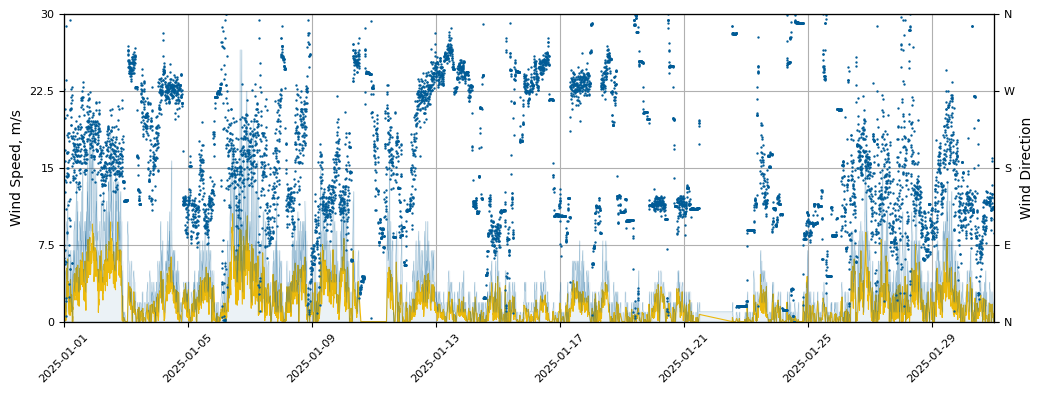
Below graphs show the wind speed and direction trneds.

Wind Speed & Direction - January

Wind Direction Distribution - January

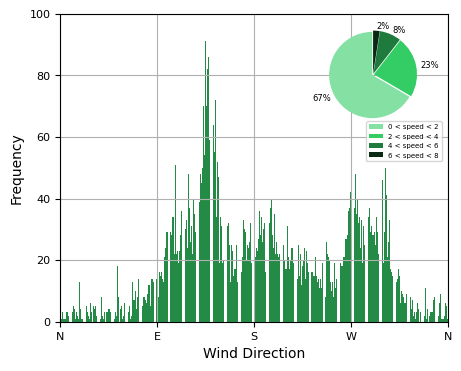
• ●The wind speed data indicates that January is a relatively stable month with a generally good average wind speed, even though 67% of wind speeds are below 2 m/s.
• ●Wind direction although follows general yearly trend - is more shifted towards the 125° in January.
• ●There is significant amount of wind gust, reaching speeds of up to 30 m/s.

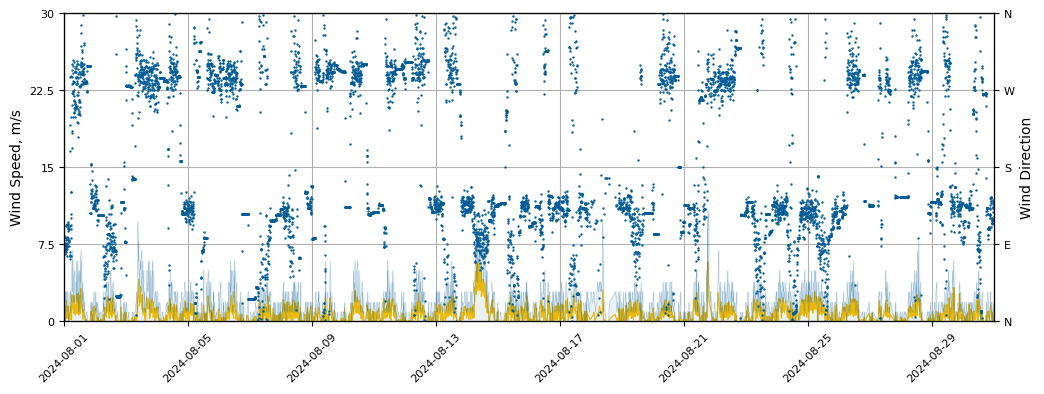
Wind Speed & Direction - August

Wind Direction Distribution - August

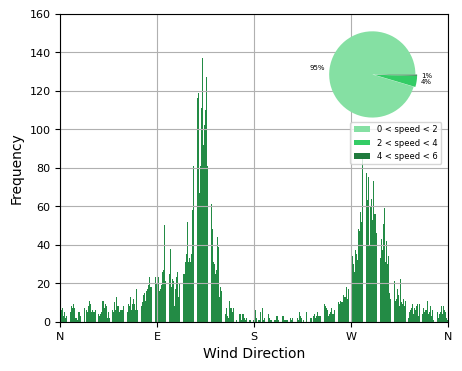
• ●Very calm month with respect to wind potential - 95% of wind speeds are below 2 m/s.
• ●Wind direction strongly correlates with general yearly trend.
• ●Overall poor wind gust being slightly height then wind speed itself.

Power Generated by a Wind Turbine Estimation

To estimate the amount of energy, that could have been generated by a wind turbine based on measured data, the following equation will be used:

where η_{gearbox/generator} - combined efficiency of the gearbox and generator (85%); C_p - desired power coefficient (40%); ρ - air dencity, kg/m³; V -wind speed, m/s; D - diameter of the wind turbine disk, m;

The air density, which is the only missing value in the equation, can be expressed by the following formula:

where t - temperature, °C; P - pressure, Pa; Rh - relative humidity, %.

Based on recent technological advancements in wind energy, and considering the installation capacity required for a given household, we consider a wind turbine height of 9 meters and a rotor diameter of 5.6 meters.

The following graphs show the monthly wind power distribution calculated considering the wind direction aligned with the turbine (115° < wind direction < 135°):

Wind Power Distribution

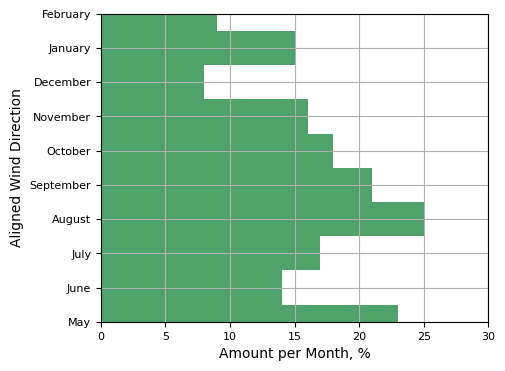
Positive Wind Direction Distribution